زمینسنجی (Geodesy) به مطالعۀ شکل و اندازه زمین و ناهمگونیهای موجود در میدان گرانشی آن میپردازد. در اول تصور میشد زمین مسطح باشد، ولی سرنخهای متعدد – نظیر ناپدید شدن کشتیها در افق، رفتهرفته این دیدگاه را اصلاح کرد و تقریباً همه متقاعد شدند که زمین گرد است. در قرن سوم میلادی، اراتوستن یونانی برآورد صحیحی از محیط زمین ارائه کرد.
رنه دکارت، فیلسوف نامدار فرانسوی، ایدۀ خارقالعادهای را مطرح نمود که به وی اجازه میداد به هر نقطۀ معین بر روی یک صفحه، نام منحصربهفردی نسبت دهد. او نقطهای روی صفحه میگذاشت و آن را مبدأ میخواند، و سپس دو محور عمود بر هم روی صفحه رسم میکرد که هر دو از مبدأ عبور میکردند. فاصلۀ هر نقطۀ معین از این دو محور با دو عدد به صورت (x, y) مشخص میشد که ما امروزه این دو عدد داخل پرانتز را مختصات دکارتی (Cartesian coordinates) مینامیم. به همین ترتیب، کل مجموعه نقطهها و دو محور عمود بر هم نیز، دستگاه مختصات دکارتی نامیده میشود. در این دستگاه، هر نقطۀ موجود بر روی صفحه آدرس مخصوص خود را دارد. دو عدد x و y امکان محاسبۀ فاصله صحیح نقطه را از مبدأ فراهم میکند. این فاصله را خیلی راحت میتوان با استفاده از قضیه فیثاغورث محاسبه نمود.
بیشتر بخوانید:
- نظریهپردازان توطئه مسطح بودن زمین را اثبات میکنند!
- طولانیترین مسیر دریایی بدون توقف از کجا عبور میکند؟
- “کنش شبحوار از راه دور” اینشتین در اجسامی که با چشم دیده میشوند، اثبات شد
ایده دکارت توانست طی سالهای بعد پیوند قدرتمندی را بین جبر و هندسه برقرار سازد.
هندسه ریمانی
برنهارت ریمان (Bernhard Riemann) در قرن نوزدهم متوجه شد که قضیه فیثاغورث به غایت تعمیمپذیر است. وی نقاطی را در یک فضای چند بعدی فرض کرد و به این فضا یا خمینه (manifold) اجازه داد انحنا بردارد، به طوری که دیگر مثل صفحه اقلیدسی مسطح نبود. ریمان در ادامه توانست فاصله بین دو نقطه معین در خمینه خود را توصیف نماید. توصیف ریمان از فاصله بین نقطهای نیز از قضیه فیثاغورث تبعیت میکرد، منتهی در مقیاسی بسیار وسیعتر از آنچه بر صفحه حاکم است.
ملموسترین راه برای درک کردن این خمینه، تجسم نمودن سطح زمین است. هندسه اقلیدسی به ما میگوید که کوتاهترین فاصله بین دو نقطه، یک خط راست میباشد. از همین رو، کوتاهترین فاصله بین دوبلین (پایتخت ایرلند) تا ملبورن، خط راستی است که از مرکز زمین عبور کند. ولی طی کردن این مسیر در واقعیت کمی دشوار است! ما در عمل قادریم روی زمین (زمینی) و یا کمی بالاتر از سطح آن (هوایی) طی مسیر کنیم. بنابراین، کوتاهترین مسیر بین این دو شهر یک دایره بسیار بزرگ است که مرکز آن روی مرکز زمین قرار میگیرد و ما در محیط (کمان) طی مسیر کرده و بین این دو نقطه جابهجا میشویم. به چنین مسیری ژئودزیک (geodesic) گفته میشود، که در تعریف، همان کوتاهترین خط مابین دو نقطه میباشد.
عدم کرویت زمین
ولی میدانیم که زمین کاملاً کروی نیست. مناسبترین بیان ریاضیوار جهت توصیف نمودن شکل زمین “کره مسطح شده” (flattened sphere) یا کرهگون (oblate spheroid) میباشد. در سال ۱۷۳۵، آکادمی علوم فرانسه سفری را به منظور تعیین نمودن دقیق شکل زمین ترتیب داد. هدف از انجام این سفر دریایی، اندازهگیری قوس مریدین (meridian arc) در دو ناحیه قطب و استوا بود. مشاهدات صورت گرفته در این سفر نشان داد که زمین شکلی شبیه به پرتقال (مسطح در دو سر و برآمده در میانه) دارد و مانند لیمو، کشیده نیست. (شاید شما هم مثل من به این قضیه توجه نکرده باشید که لیمو گرد نیست، بلکه کشیده است).
بیشتر بخوانید:
- داستانهای ناگفته: روزی که زمین تکان خورد
- شگفت انگیزان ۲: روش درست برای حل یک مسئله ریاضی کدام است؟
- مسئله تراموا برای اولین بار در زندگی واقعی آزمایش شد
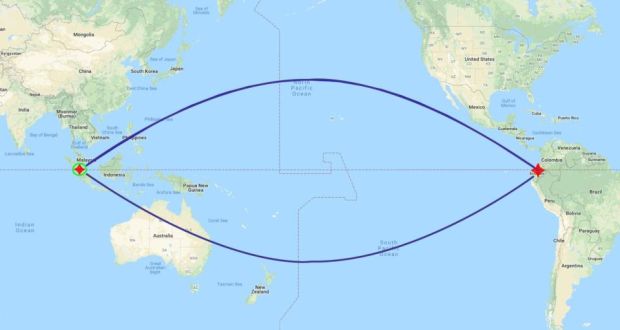
به استثنای دو نقطه متقاطر (antipodal)، فاصلۀ بین هر دو نقطۀ معین واقع بر روی ژئودزیک منحصربهفرد است، و یا به عبارت دیگر، یک عدد واحد میباشد. با این حال، هنگامی که مختصر مسطح شدگی زمین دو در قطب را نیز وارد کار میکنیم، اتفاق عجیبی روی میدهد: فاصله بین دو نقطه دیگر یک عدد واحد و منحصربهفرد نیست! برای مثال، سنگاپور و کیتو (پایتخت اکوادور) هر دو بر روی خط استوا قرار دارند، ولی برآمدگی زمین در استوا موجب شده است که خط استوا، به شخصه، کوتاهترین فاصله بین این دو شهر محسوب نشود. در حقیقت ما در این جا نه یک، بلکه دو مورد کوتاهترین مسیر بین سنگاپور و کیتو داریم؛ که یکی از بالای هاوایی عبور کرده و دیگری از پایین خلیج کارپنتاریا رد میشود (در اینجا منظور از بالا و پایین، عرض جغرافیایی است).
با این که اثر عدم کرویت زمین (nonsphericity) چندان چشمگیر نیست، ولی با توجه به قیمت سوخت، عدم کرویت زمین در پروازهای دوربرد نمود برجستهتری پیدا میکند. عدم کرویت زمین همچنین آثار قابل تأملی روی اخترشناسی، اندازهگیری زمین، نقشهبرداری از معادن، تعیین موقعیت ماهوارهها و GPS دارد.
