پاسخ به سه معمای هندسه که از کتاب Geometry Snacks برای‌تان آورده بودیم.
۱. مثلث قرمز چه کسری از مساحت مثلث بزرک را تشکیل داده است؟
پاسخ: ۰/۲۵
این مسئله را می‌توان به حداقل ۳ روش حل نمود.
روش اول: اگر مثلث بزرگ را به ۸ مثلث هم‌سان تقسیم کنیم، به راحتی می‌توانیم نتیجه بگیریم که مثلث قرمز دو واحد از مثلث‌های کوچک‌تر را می‌پوشاند؛ که می‌شود یک‌چهارم مساحت مثلث بزرگ.
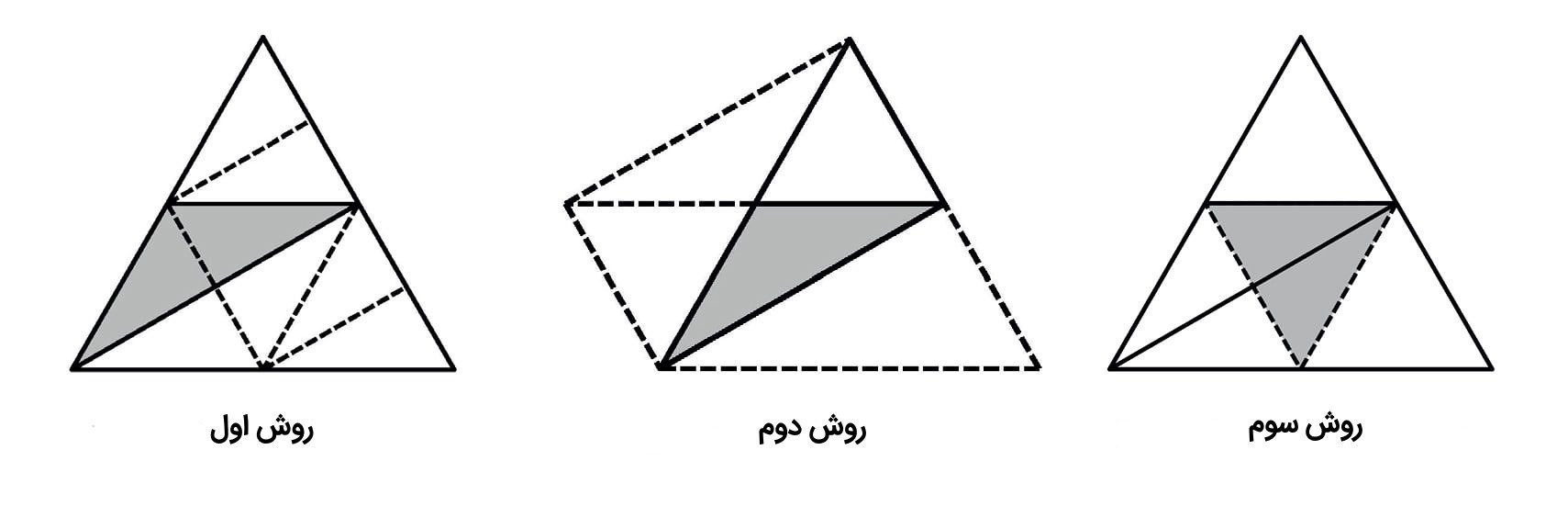
روش دوم: می‌توان با امتداد دادن یکی از اضلاع مثلث قرمز از نقطۀ وسط ساق مثلث بزرگ و وصل نمودن دو رأس به آن، شکلی شبیه به پاکت نامه ایجاد نمود که مساحتی برابر با مساحت مثلث بزرگ دارد. مشاهده می‌کنید که مثلث قرمز، ربغ مساحت این پاکت نامه را تشکیل می‌دهد.
روش سوم: در صورتی که مثلث بزرگ را به ۴ مثلث هم‌سان تقسیم کنیم، خواهیم دید که مساحت مثلث قرمز با مساحت یکی از این مثلث‌های جدید برابر است.
۲. چهار نیم‌دایره به شعاع ۲ سانتی‌متر مطابق زیر در داخل یک مربع چیده شده‌اند. مساحت مربع چقدر است؟
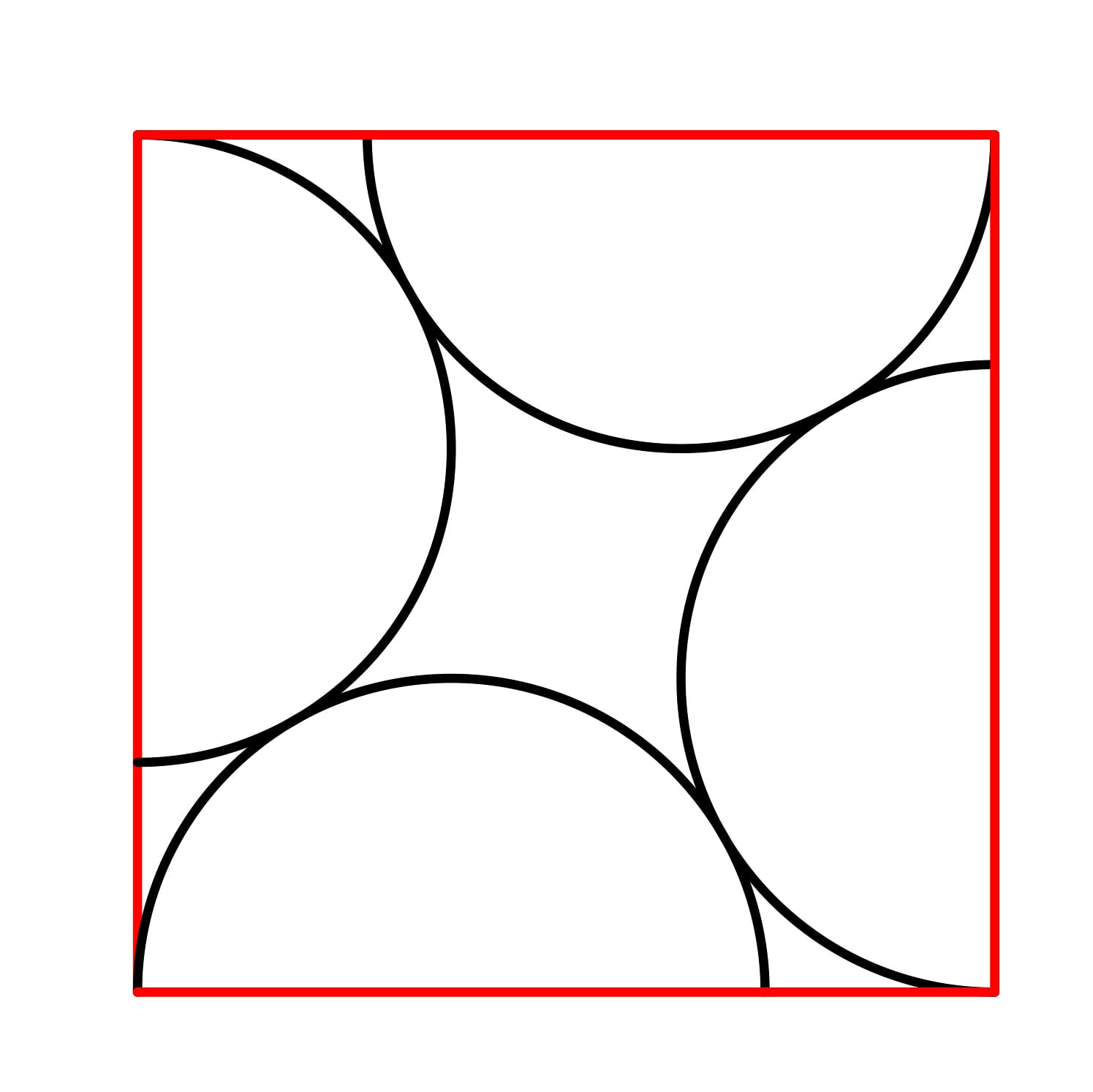
پاسخ: ۸(۲ + ۳√)
برای حل این یکی باید با اصل فیثاغورث آشنایی داشته باشید. بر اساس این اصل، مجموع مربع‌های اضلاع قائم یک مثلث قائم‌الزاویه با مربع وتر آن برابر است.
روش اول: به مثلث قائم‌الزاویه‌ای که در تصویر بالا (سمت چپ) برای‌تان رسم کرده‌ایم دقت کنید. طول وتر این مثلث برابر با ۴ سانتی‌متر است (۲ برابر شعاع دایره) و اندازه یکی از اضلاع آن نیز ۲ سانتی‌متر می‌باشد (شعاع دایره). اگر اندازۀ ضلع سوم را x فرض کنیم، در آن صورت خواهیم داشت:
x۲ + ۲۲ = ۴۲ که در صورت ساده‌سازی می‌شود: x۲ = ۱۶ – ۴ = ۱۲
حاصل x برابر است با جذر ۱۲: ۳√۲
همان‌طور که می‌دانیم ضلع مربع برابر است با حاصل x + 2 که با توجه به معادله بالا برابر خواهد بود با: ۲ + ۳√۲
در صورتی که ضلع مربع را به توان ۲ برسانیم، مساحت آت را خواهیم داشت:
(۲ + ۳√۲)۲ = ۴ + ۳√۸ + ۱۲ = ۱۶ + ۳√۸ = ۸(۲ + ۳√)
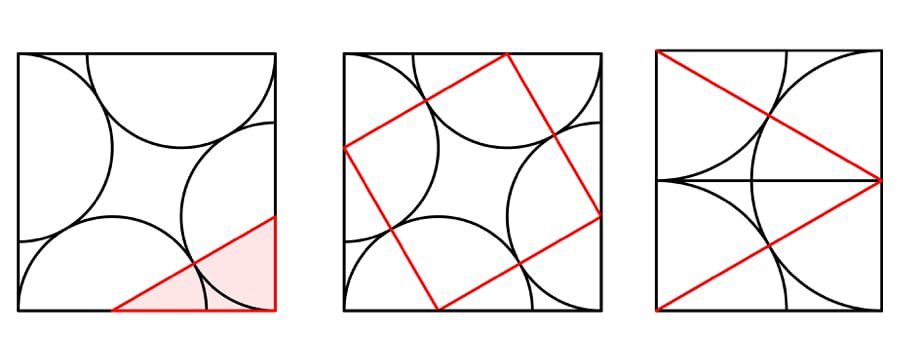
روش دوم: به تصویر وسط (بالا) توجه کنید. در این شکل، مربع قرمز رنگی را با اتصال مراکز نیم‌دایره‌ها در داخل مربع بزرگ ترسیم کرده‌ایم. حال اگر این ۴ مثلث خارج از مربع قرمز را جابه‌جا کرده و به یک‌دیگر بچسبانیم، شکلی همانند تصویر راست حاصل خواهد شد (این کار را روی کاغذ انجام دهید). مستطیل حاضل طول و عرضی برابر را ۴ و ۳√۲ خواهد داشت. مساحت مربع بزرگ در این حالت، برابر است با مساحت مربع قرمز به اضافه مساحت مستطیل (که از ۴ مثلث تشکیل یافته). با کمی محاسبه به همان جواب قبل خواهید رسید.
۳. ربع دایره‌ای به شعاع ۶ سانتی‌متر در زیر نشان داده است. داخل آن، دو نیم‌دایره و یک دایره به صورت مماس بر هم رسم شده است. شعاع دایره و نیم‌دایرۀ کوچک‌تر چقدر است؟
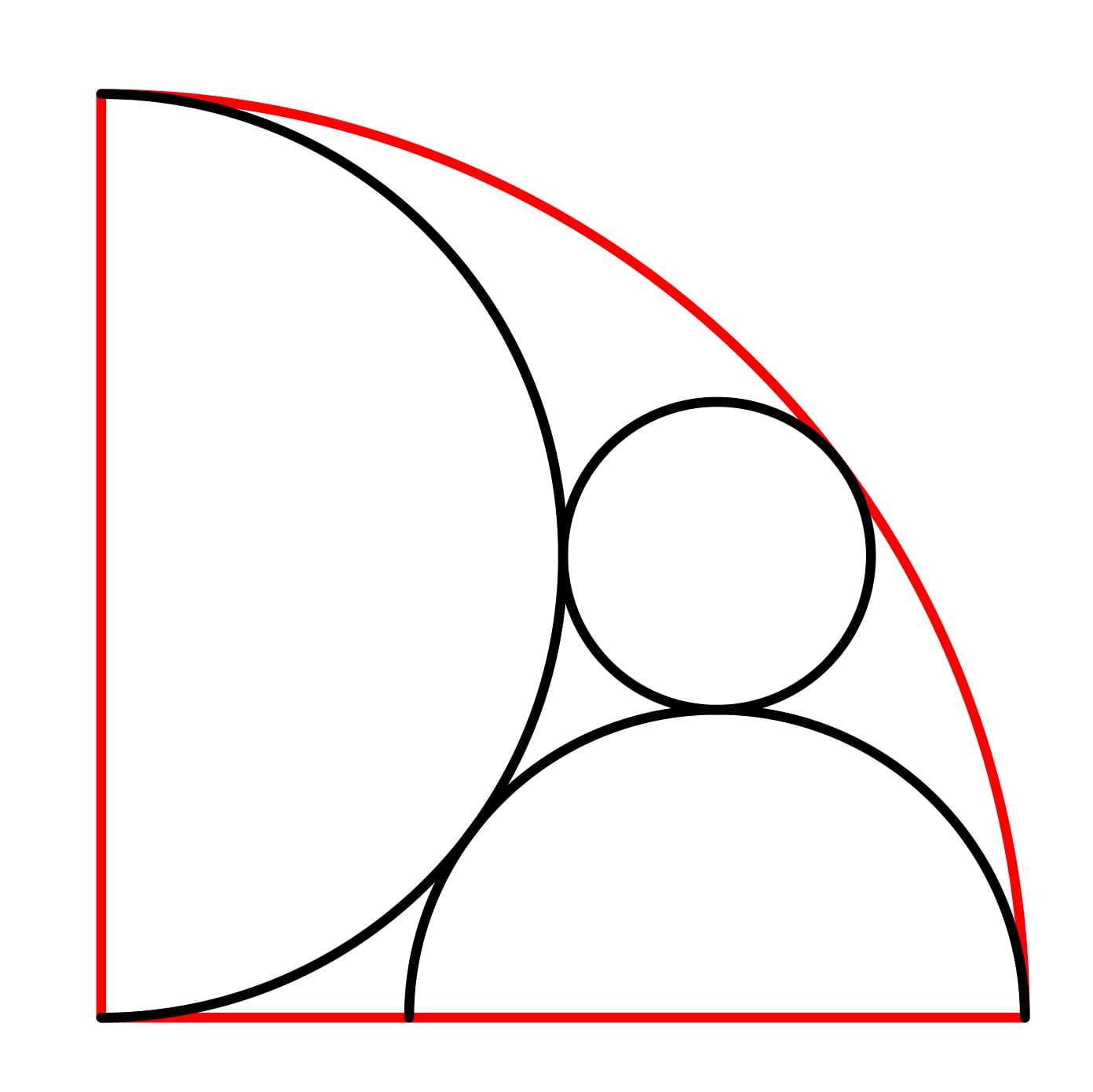
پاسخ: شعاع دایره ۱ و شعاع نیم‌دایرۀ کوچک برابر با ۲ سانتی‌متر است.
برای حل، شعاع دایره را برابر با r و شعاع نیم‌دایرۀ کوچک‌تر را R در نظر می‌گیرم. از آن‌جایی که شعاع ربع دایره برابر با ۶ است؛ شعاع نیم‌دایرۀ بزرگ‌تر ۳ سانتی‌متر خواهد بود.
روش حل: مثلث قائم‌الزاویه‌ای را که در شکل روبه‌رو مشخص شده، در نظر بگیرید. طول وتر این مثلث برابر است به ۳ + R. اضلاع قائم نیز اندازه‌هایی برابر با ۳ و r + 3 خواهند داشت. از فیثاغورث داریم:
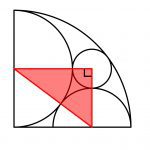
۳۲ + (r + ۳)۲ = (۳ + R)۲
و هم‌چنین می‌دانیم: r + R = 3 و یا r = 3 – R که در ادامه خواهیم داشت:
۳۲ + (۶ – R)۲ = (۳ + R)۲
بنابراین R = ۲ و r = ۳ – R = ۱ خواهد بود.
