هفتهی قبل با خبرهای خوبی برای علاقهمندان به علم ریاضی همراه بود. در ابتدا باخبر شدیم که ابررایانهها پرده از پاسخ یک معمای ۶۵ ساله برداشتهاند. این معمای بسیار معروف یک «معادله سیاله» بود، که در آن حاصل جمع مکعبهای x، y و z برابر با k است. برای مطالعهی خبر مربوط به حل این معمای ریاضی میتوانید به وبسایت «Popular Mechanics» مراجعه کنید.
صرف نظر از حل این معادلهی درجه سوم، شنیدهها حاکی از آن است که «ترنس تائو» به پاسخ یک معمای ۸۲ ساله در علم ریاضی، نزدیک شده است.
ترنس تائو از ریاضیدانان بزرگ زمان ماست. او در ۲۱ سالگی توانست مدرک دکترای تخصصی خود را از دانشگاه پرینستون اخذ نماید. تائو به عنوان جوانترین استاد ریاضی در دانشگاه کالیفرنیا شناخته میشود. وی در سال ۲۰۰۶ موفق به کسب «مدال فیلدز» شد. مدال فیلدز بزرگترین جایزهی علمی در حوزهی ریاضیات است، و به نوعی میتوان آن را نوبل ریاضی خواند. تائو در آن زمان تنها ۳۱ سال داشت.
پیشنهاد نویسنده: هفت برندهی مدال فیلدز که باید بشناسید!
او هماکنون در ۴۴ سالگی، خبرهای خوبی در مورد یکی از دشوارترین معماهای ریاضی منتشر کرده است.
معمای مورد بحث «حدس کولاتز» نام دارد. این معما که یکی از گزارههای اثبات نشده در علم ریاضی است، برای اولین بار در سال ۱۹۳۷ توسط ریاضیدان آلمانی، «لوتار کولاتز» مطرح گردید. حدس کولاتز تقریباً برای هر دانشآموزی قابل فهم است. این معما علیرغم ظاهر سادهای که دارد، پس از گذشت ۸۲ سال هنوز حل نشده است.
حدس کولاتز چیست؟
حدس کولاتز به شکل زیر تعریف میشود:
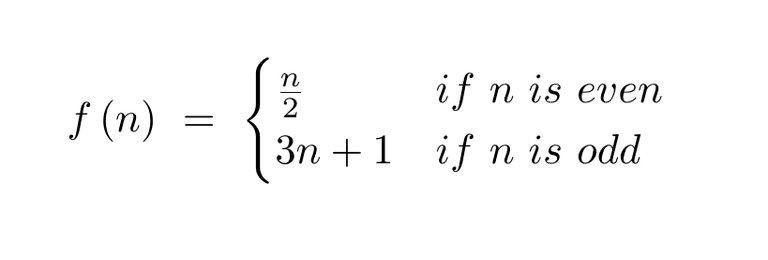
این حدس تنها از دو قانون اصلی تشکیل شده است. مطابق معمول، n برابر است با هر عدد طبیعی دلخواه. مطابق با قانون اول، در صورتی که n یک عدد زوج باشد، باید آن را بر ۲ تقسیم کنیم. بند دوم میگوید که اعداد طبیعی فرد باید ابتدا در ۳ ضرب شده و سپس با یک جمع شوند.
فرقی ندارد چه عددی را برای حل این معما انتخاب میکنید، مهم آن است که عدد به دست آمده از یک معادله، بلافاصله وارد معادلهی دیگر میشود، تا به جواب نهایی برسیم. آن چه که باعث شده حدس کولاتز به یک معمای غیر قابل حل تبدیل شود، این است که فرقی ندارد چه عددی را وارد این حدس بکنید، مقدار نهایی این تابع همواره «یک» خواهد بود. بیایید با یک مثال بررسی کنیم.
برای شروع، عدد ۱۰ را انتخاب میکنیم. ۱۰ یک عدد زوج است، بنابراین با پیروی از قانون اول، آن را به ۲ تقسیم میکنیم. عدد حاصل ۵ خواهد بود. ۵ فرد است، بنابراین باید وارد معادلهی دوم شود. حاصل این معادله ۱۶ خواهد بود. حال باید چرخه را ادامه دهیم، و ۱۶ را به ۸ نصف کنیم. ۸ زوج است و دوباره وارد همین معادله شده، و به ۴ تبدیل میشود. پس از چهار، عدد ۲ و در نهایت «یک» را خواهیم داشت.
با هر عدد طبیعی دیگری که شروع کنید، دوباره به همین «یک» خواهید رسید. میتوانید امتحان کنید. این معما حدس کولاتز نام دارد.
تا جایی که ما میدانیم، حدس کولاتز برای تمام اعداد طبیعی با کمتر از ۱۹ رقم، پاسخ یکسانی دارد. این منتهیالیه مسیری است که ما میتوانیم طی کنیم. حال اگر این معما را در اختیار ابررایانهها قرار دهیم، به نتیجهی مشابهی برای اعداد طبیعی با ۱۰۰ الی ۱۰۰۰ رقم خواهیم رسید! یعنی این اعداد بسیار بزرگ هم پس از عبور از حدس کولاتز به «یک» تجزیه خواهند شد.
پیشنهاد نویسنده: بزرگترین عدد اول با بیش از ۲۳ میلیون رقم کشف شد!
تاکنون خبر جدیدی در مورد حل این معما مطرح نشده بود. به تازگی، ترنس تائو پست جدیدی را در وبلاگ شخصی خود منتشر کرده، که به حدس کولاتز ارتباط دارد. او در این پست گفته که «تقریباً همهی مدارهای کولاتز به مقادیر نسبتاً جفتشده منتهی میشوند».
حال، ابتدا باید با مفهوم «مدار کولاتز» آشنا شویم، که اتفاقاً بسیار ساده است. مدار کولاتز به توالیهای خاصی اطلاق میگردد، که از هر عدد طبیعی خاص در این معادله حاصل میشود. برای مثال، مدار کولاتز عدد ۱۰ عبارت است از:
۱۰, ۵, ۱۶, ۸, ۴, ۲, ۱, ۴, ۲, ۱, …
بنابراین، مدار کولاتز از همهی عددهایی تشکیل میشود، که به عنوان جواب برای یک عدد طبیعی خاص به دست میآیند. از آنجایی که پاسخ نهایی برابر با یک است، مقدار معادلهی دوم (۳n + 1) برابر با ۴ خواهد بود. این چهار نیز بر اساس معادلهی به ۲ خواهد رسید. بنابراین، تمام مدارهای کولاتز به توالی (۱، ۲، ۴) ختم خواهند شد. این توالی سهتایی تا ابد در داخل حدس کولاتز ادامه پیدا خواهد کرد. این از مفهوم مدار کولاتز.
نکتهی مهم دیگر در مورد ادعای ترنس تائو، الفاظ «تقریباً» و «نسبتاً» است. «تقریباً» معمولاً حکم آخرین مانع در رسیدن به جواب یک معادله را دارد. این لفظ در زمینههای گوناگون ممکن است معانی متفاوتی داشته باشد. اما منظور تائو از «تقریباً» چه بوده است؟
«تقریباً» در این بیان به مفهوم «تراکم لگاریتمی» است. به عبارت دیگر، منظور تائو این است که احتمال پیدا کردن عددی که بتواند جواب نهایی حدس کولاتز را نقض کند، بسیار کم است. چنین عدد یا عددهایی ممکن است وجود داشته باشد، اما با پیشروی در مسیر اعداد طبیعی، فراوانی چنین عددی به صفر میل میکند. هدف تائو اثبات این قضیه است که چنین عددی عملاً وجود ندارد.
مطابق با فرضیهی تائو، احتمال کشف مثال ناقض برای حدس کولاتز بینهایت کم است. باید توجه کرد که حتا «بینهایت کم» با «صفر» تفاوت دارد، و همچنان احتمال وجود داشتن چنین عددی فراهم است.
خب، اکنون که احتمال وجود مثال ناقض در این معادله به حداقل میزان خود رسیده، آیا حدس کولاتز را باید حل شده به حساب بیاوریم؟
پاسخ کاملاً مثبت نیست. ولی میتوان ادعا کرد که تا چند دههی آینده، حدس کولاتز همچنان یک حدس باقی خواهد ماند. چون ما هنوز نتوانستهایم احتمال وجود مثال ناقض را برای آن کاملاً رد کنیم.

این سوال که خیلی ساده است
شما دقت کنید
مکانیسم این اینجوریه
اگه عدد زوج بود تقسیم بر دو میکنیم
اگه زوج نبود به زوج تبدیلش میکنیم و تقسیم بر دو میکنیمش
و اینم مشخصه که همیشه به یک میرسه و هیچ استثنایی هم نداره
چون در هر حال عدد یا زوج میشه یا به زوج تبدیل میشه
یعنی شما به جای عدد سه،هر عدد فردی که دلت بخواد میتونی بذاری و همینجوری میشه؛هیچ محدودیتی هم در انتخاب عدد فرد وجود نداره
میتونید امتحان کنید
خب شما فرض کن به یه عدد فرد رسیدیم بعد تبدیل به زوج شد
بعد از اون احتمال داره که عدد زوج بدست اومده دوباره به فرد تبدیل باشه
و چون در فرد هاضربدر ۳ میکنیم ولی درزوج ها ضربدر ۲ میکنیم پس
هر دفعه ای که به یه عدد فرد میرسیم مسئله نسبت به دفعه پیش سخت تر میشه
میشه و احتمال اینکه دوباره و دوباره به یه عدد فردغیر یک برسیم بیشتر میشه
خب این سوال آدم رو فریب میده ما جواب نهایی نداریم که بخواهیم روش متمرکز شیم.یک عددی فرده وعملیات رو روش انحام میدیم باز مراحلی تکرار میشه.در واقع این سوال برای درگیر افکارات طرح شده.البته این نظر منه
سلام.این یه سوال فریب دهنده است فک کنم اصلا باسه این طراحی شده چون عدد نهایی نداریم خب میرسیم به یک خب باز یه عملیاتی اعمال می کنیم تکراری.البته این نظر منه