بحث را با یک سوال ساده شروع میکنیم: ماشین شما بنزین تمام کردهاست. چقدر نیرو لازم دارید تا ماشین را به یک سرعت معین شتاب دهید؟ جواب با قانون دوم نیوتون به راحتی حاصل میشود: F=ma.
که در این فرمول a شتاب، F نیرو و m جرم را نشان میدهد. یک قانون جمع و جور و حسابشده که حداقل از لحاظ تئوریک میتواند به همه سوالات فیزیکدانان پاسخ دهد.
یا حداقل تا چند دهه قبل این طور فکر میکردند، تا زمانی که سروکار آنها با پدیدههای فیزیکی در مقیاس بسیار ریز افتاد، مثل گردش یک الکترون دور هسته یک اتم که فهمیدند اوضاع در این مقیاس آنقدر عجیب و غریب است که دیگر قوانین نیوتن پاسخگو نمیباشد. برای توصیف این دنیای بسیار ریز به مکانیک کوانتومی نیاز داشتند، تئوری که در اوایل قرن بیستم تدوین شد. معادله بنیادین این تئوری، که با قانون دوم نیوتون همانندی دارد، معادله شرودینگر نامیده میشود.
ذرات و امواج
در مکانیک کلاسیک، وضعیت یک سیستم فیزیکی را با مکان و تکانه آن توصیف میکنیم. برای مثال یک میزی را در نظر بگیرید که پر از توپهای بیلیارد است که در حال حرکتند و شما مکان و تکانه هر توپ را در زمان t میدانید و با این دو همه چیز درباره این سیستم مشخص میشود: توپها در لحظه t کجاهستند، کجا قرار است باشند و با چه سرعتی حرکت میکنند. ما از وضعیت سیستم درT۰ خبر داریم و با قانون دوم نیوتون سیر دینامیکی آن نیز مشخص است. ولی وقتی بحث مکانیک کوانتوم برای همان سوال مطرح میشود اوضاع یکم پیچیده است چون مکان وتکانه یک سیستم با متغیرهای درستی توصیف نمیشود.
مشکل این است که در مکانیک کوانتوم اشیا همانند توپهای بیلیارد عمل نمیکنند. بعضی وقتها بهتر است انها را به شکل امواج در نظر بگیریم. برای مثال نور را در نظر بگیرید. نیوتون علاوه بر جاذبه به نور نیز علاقه مبرم داشت و آن را ذره در نظر میگرفت. ولی بعدها با تلاش فیزیکدانان مختلف مثل درک تئوریکی که توسط James Clerk Maxwell ارائه شد، نور را موج در نظر گرفتند.
ولی درسال ۱۹۰۵ انیشتین متجه شد که انگاره موجی بودن نور هم تصویر دقیقی از آن را ارائه نمیدهد. برای توجیه پدیده فتوالکتریک، شما باید نور را مثل جریانی از ذرات در نظر بگیرید که انیشتین انها را فوتون نامید. تعداد فوتونها متناسب با شدت نور است و انرژی E هر فوتون با فرکانس F ان متناسب است: E=hf.
که در این فرمول h ثابت پلانک است. به هر حال در پایان نتیجه این شد که بهتر است برخی مواقع نور را موج و برخی مواقع ذره در نظر گرفت. نتایج انیشتین با یک سیری از مطالعات علمی مرتبط است که با Christiaan Huygens در قرن هفدهم شروع شد و در قرن ۱۹ William Hamilton دوباره به آن میپرداخت: ادغام فیزیک نوری (که با امواج مرتبط بود) با مکانیک (که با ذرات مرتبط بود). فیزیکدان فرانسوی Louis de Broglie با الهام از رفتار شیزوفرنیک نور گامی مهم را در این مسیر برداشت: او فرض کرد که نه تنها نور بلکه ماده نیز این دوگانگی موج و ذره را دارد. اجزای سازنده ریز ماده مثل الکترونها هم برخی اوقات مثل ذرات و برخی اوقات مثل امواج عمل میکنند.
عقیده De Broglie که در دهه ۲۰ مطرح شد، براساس شواهد ازمایشی نبود و محتوای تئوریک نسبیت عام انیشتین الهام گرفته شدهبود. ولی شواهد کمی بعد از ان فراهم شد. در اواخر دهه ۲۰ ذرات عبورکننده از کریستال ماهیت ذرهای الکترونها را تایید کرد.
یکی از معروفترین نمودهای ماهیت موجی-ذرهای، آزمایش شکاف دوگانه است. در ان الکترونها به یک صفحه که دو شکاف دارد پرتاب میشوند. پشت آن یک صفحه دیگر وجود دارد که نشان میدهد الکترونها به کجا رسیدهاند. اگر الکترونها مثل ذرات رفتار کنند، بنابراین انتظار خواهید داشت که که دو خط را پشت صفحه تصویر کنند. ولی آنچه که شما در آن صفحه میبینید، یک الگویی شبیه تداخل امواج است: که در ان الکترونها همانند امواج عمل میکنند و هر موج از هر دو شکاف رد میشود و در صفحه پشتی با خود تداخل مییابد و به طرف دیگر پخش میشود. از طرف دیگر بر روی صفحه ردیاب هنگام رسیدن به آن همان الگوی ماهیت ذرهای را هم بروز میدهند. آزمایش نتایج عجیبی را در برداشت، ولی خب باید قبول کرد دنیا به این منوال است.
معادله شرودینگر
تصویر جدیدی که de Broglie ارائه دادهبود، نیازمند فیزیک جدید بود. توصیف ریاضیوار موجی که با ذره مرتبط است چگونه میباشد؟ انیشتین قبلا انرژی E یک فوتون را با فرکانس F نور مرتبط ساختهبود، که در مقابل با توجه به فرمول c/f=λ با طول موج λ نیز مرتبط است.
تئوری نسبیت ارتباط انرژی یک فوتون را با تکانه آن ممکن ساختهاست. با درنظر گرفتن همه اینها این رابطه بین طول موج λ با تکانه p بدست میآید(h ثابت پلانک است): λ=h/p.
بر این اساس، de Broglie فرض کرد که همین رابطه باید میان طول موج و تکانه هر ذرهای صادق باشد.
در این نقطه بهتر است فعلا از تفکر در مورد اینکه یک ذره چگونه میتواند رفتار موجی داشتهباشد را فعلا کنار بگذارید و به ریاضیاتی که در ادامه آوردهایم توجه کنید.
در ریاضیات کلاسیک سیر تکاملی یک موج در گذر زمان با یک معادله موجی مشخص میشود: یک معادله دیفرانسیل که راهحل آن یک تابع موجی است و شکل کوج را در هر tای میتواند توصیف کند( مشروط به شرایط مناسب کرانی).
برای مثال، فرض کنیم شما امواجی دارید که در راستای محور X جابهجا میشود و در صفحه XY نوسان دارد. برای اینکه موج را به طور کامل توصیف کنیم، شما نیاز دارید تا این جابهجایی (y(x,t در راستای y را به ازای هرx و هر t بدست بیاورید. با استفاده از قانون دوم نیوتون، میتوانید نشان دهید که (y(x.t از معادله موجی زیر پیروی میکند:
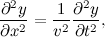
که در اینجا v سرعت را نشان میدهد.
یک راهحل عام برای (y(x.t کمی پیچیده است، که نشاندهنده این حقیقت است که چون حرکت در همه جهات صورت میگیرد، نیازمند اطلاعات بیشتر برای درک ماهیت حرکت هستیم. ولی برای مثال این تابع
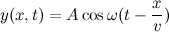
نشان میدهد که موج در جهت مثبت با فرکانس زاویهای ω سیر میکند، همانطور که انتظار داشتید یک راهحل ممکن برای معادله موجی است.
به طور مشابه، باید یک معادله موجی هم برای این امواج ذرهای مرموز هم باشد. راهحل ان یک تابع موجی Ѱ است(توجه کنید که یک موج حقیقی را توصیف نمیکند) که به شما انچه را که باید در مورد سیستم کوانتومی آن باید بدانید، میگوید. برای مثال، یک ذره منفرد که در هر tای درون جعبهای حرکت میکند. فیزیکدان اتریشی اروین شرودینگر معادله زیر را در سال ۱۹۲۶ ارائه داد. به ازای هر ذره منفردی که در سه بعد مختلف حرکت میکند میتوان معادله را به صورت زیر نوشت:
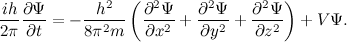
در این معادله V انرژی پتانسیل ذره ، i=√-۱ ، جرم ذره m وh ثابت پلانک است. راه حل این معادله به صئرت تابع موجی x,y,z,t)Ѱ) میباشد.
در برخی مواقع انرژی پتانسیل به t بستگی ندارد. در این موارد ما میتوانیم مسئله به وسیله فرم مستقل از زمان معادله شرودینگر حل کنیم:
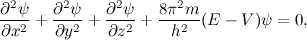
که در ان E انرژی کل ذره است. راه حل Ѱ برای معادله کامل آن به این صورت است:
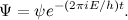
این معادلات برای یک ذرهای که در ۳ جهت حرکت میکند کاربرد دارد ولی نمونههای مشابهی برای توصیف سیستمی با هرچند ذره دلخواه نیز وجود دارد. و به جای اینکه تابع موج را با پارامترهای مکان و زمان فرمولبندی کنید، میتوانید از تکانه و زمان نیز استفاده کنید.
عدم قطعیت وارد میشود
این معادله واقعا به چه معناست؟ مکان دقیقی از ذره را در زمان داده شده نمیدهد بنابراین خط سیر ذره را حین گذر زمان نمیدانید. به جای آن، این یک تابعی است که به شما به ازای t داده شده، مقدارx,y,z,t)Ѱ) را در هر (x,y,z) ممکن به شما میدهد. این مقدار به چه معنا است؟ در سال ۱۹۲۶، Max Born فیزیکدان یک تفسیر احتمالگرایانه ار مطرح کرد. او فرض کرد که جذر مقدار مطلق تابع موجی:
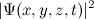
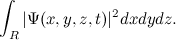
این تصویر احتمالگرایانه با سری فرمولهای دیگری از de Broglie برای طول موج و تکانه یک ذره مرتبط میشود که توسط Werner Heisenberg در سال ۱۹۲۷ یافت شد. Heisenberg پی برد که یک حد بنیادی برای اندازهگیری موقعیت و تکانه یک ذره وجود دارد که در دستاورد مربوط به آن توضیح داده شدهاست.
این معادله تا به حال از هر ازمایشی سربلند بیرون آمدهاست. و در حقیقت نقطه آغازی برای بررسی همه سیستمهای مکانیکی کوانتومی است که میخ.اهیم توصیف کنیم: الکترونها، پروتونها، نوترونها و غیره. یکی از اولین موفقیتهای معادله که به نوعی یکی از مشوقهای شرودینگر بود، توصیف پدیدهای است که در همان آغاز به تولد مکانیک کوانتومی کمک کرد: طیف انرژی گسسته اتم هیدروژن. براساس مدل اتمی رادرفورد، فرکانس تشعشعات تابششده از اتمها باید پیوسته میبود، درحالیکه ازمایشها نشان میداد که اینگونه نبود: اتم هیدروژن تنهادر فرکانسهای معینی تشعشعات خود را تابش میکند، و میان این تفییر فرکانسها جهشهای قابلتوجهی وجود دارد.
در سال ۱۹۱۳ نیلز بور مدل اتمی جدیدی را معرفی کرد که در آن الکترونها در سطوح انرژی مشخص قررا داشتند. شرودینگر معادله خود را بر روی اتم هیدروژن به کار بست و نتایج آن همان سطوح اندژی مشخص بور را نشان میداد که یکی از دستاوردهای اصلی معادله شرودینگر بود.
با داشتن موفقیتهای بیشمار در میان آزمایشهای انجامشده بر روی ان، معادله شرودینگر به عنوان همتای قانون دوم نیوتون در مکانیک کوانتوم تثبیت شدهاست.
