از منظر احتمال
فرض کنیم همانطور که در شکل (۱) نشان داده شدهاست، ظرفی به حجم V داریم که از مولکولهای یک گاز ایدهآل پر شدهاست. میدانیم که این مولکولها در فضای ظرف آزادانه حرکت میکنند، پخش میشوند و کل فضا را پر میکنند.
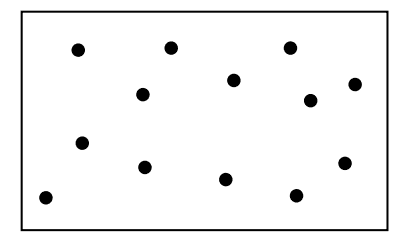
سپس همانطور که در شکل (۲) نشان داده شدهاست، تنها یک مولکول از همان ظرف را در نظر بگیرید. این مولکول آزادانه در فضای ظرف حرکت میکند.
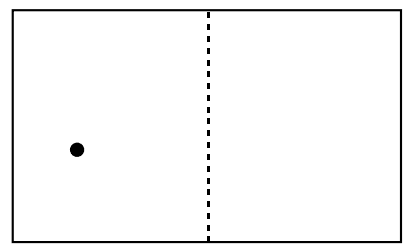
شکل ۲: یک مولکول از گاز ایدهآل در ظرفی به حجم V. خط چینی که در وسط وجود دارد، ظرف را به نیمههای مساوی نقسیم میکند.
از آنجایی که سوگیری خاصی در احتمال محل قرار گرفتن مولکول گاز وجود ندارد، احتمال (P) قرار داشتن مولکول گاز در نیمه چپ ظرف برابر است با:
P = ۱/۲
سپس همانطور که در شکل (۳) نشان داده شدهاست، دو مولکول منفرد گاز را در یک طرف ظرف در نظر بگیرید.
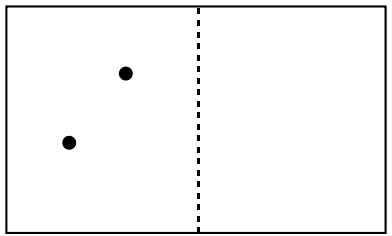
احتمال یافتن هر دو مولکول گاز ایدهآل در یک طرف ظرف برابر است با:
(۱/۴)=(۱/۲).(P=(1/2
از آنجایی که مولکولهای گازی مستقل از هم هستند، با توجه به معادله بالا، برای یافتن احتمال وجود جفت مولکولها در هر یک از نصف ظرفها باید احتمال یافتهشدن هر یک از مولکولهای منفرد را دخیل کنیم.
سپس تصور کنید ظرفی که در شکل (۱) نشان داده شدهبود، با N مولکول گاز ایدهآل پر شدهباشد(شکل ۴). مشابه موارد قبلی، میتوانیم احتمال وجود N مولکول در نصف سمت چپ ظرف را تعیین کنیم.
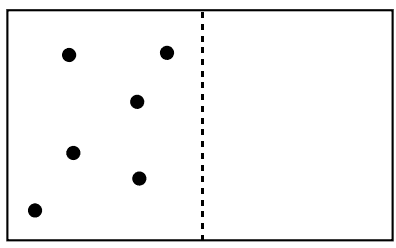
بار دیگر، با توجه به اینکه مولکولهای مستقل از هم هستند، برای بدست آوردن احتمال وجود N مولکول در نیمه چپ ظرف، با لحاظ کردن احتمال هر یک از مولکولها به دست میآید:
(P=(1/2)(1/2)…(1/2) (N factors
P=(1/2)N
جدول (۱) نمونههایی از احتمالهای حسابشده به وسیله فرمول بالا را برای حضور همه مولکولها در یک نیمه ظرف را نشان میدهد.
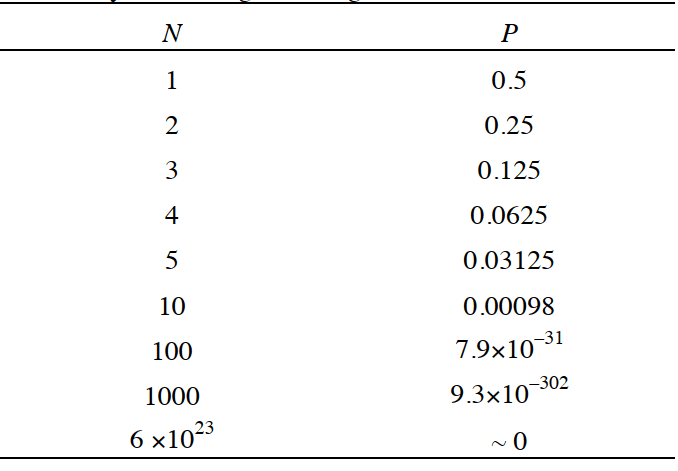
این کاهش شتابدار احتمال با افزایش N به ما کمک میکند تا بتوانیم از لحاظ آماری توجیه کنیم که چرا یک گاز برای پر کردن تمام فضای موجود منبسط میشود. مطابق شکل ۵A پیستونی را در نظر بگیرید که حجم گاز درون محفظه را به V/2 کاهش میدهد.
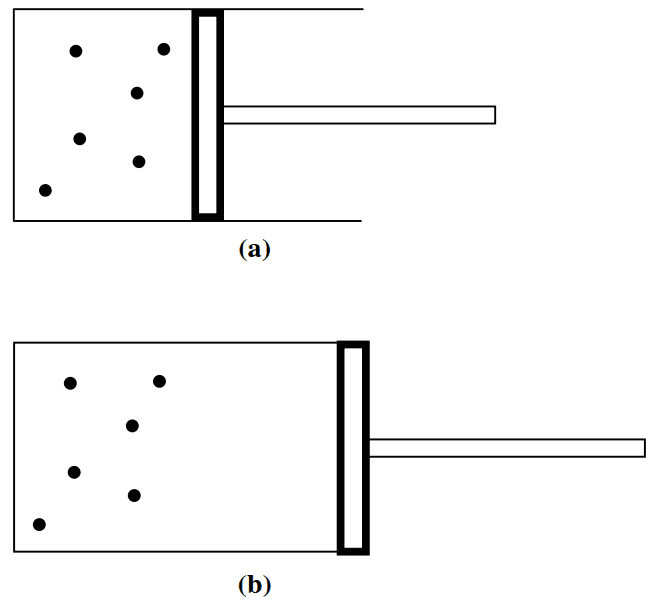
شکل ۵A: مولکولهای گاز ایدهآل توسط یک پیستون به به اندازه نصف حجم اولیه محفظه فشرده شدهاند. (B) پیستون ناگهان آزاد میشود تا مولکولها در تمام حجم محفظه پخش شوند.
پیستون ناکهان آزاد میشود تا مولکولها بتوانند تمام حجم مخفظه را پر کنند. همان طور که انتظار میرفت، مولکولهای گازی به سرعت منبسط میشوند تا بتوانند کل محفظه را پر کنند. چرا مولکولها هنگامی که پیستون آزاد میشود، در نیمهای که در آن بودند، باقی نمیمانند؟ یکی از دلایل این است که احتمال وقوع چنین رخدادی همانطور که در جدول (۱) نشان داده شدهاست، بسیار ناچیز میباشد. به عبارتی دیگر، گاز ب دنبال وضعیت پایداری است.
واکنشهای خودبهخودی
براساس نتایجی که درارتباط با مولکولهای گاز ایدهآل و احتمالات آنها گرفته شدهاست، میتوان واکنش خودبهخودی را تعریف کرد. واکنش خودبخودی فرآیندی است که در آن تغییر از وضعیتی با احتمال وقوع کم به وضعیتی با احتمال وقوع بالا صورت میگیرد.
نمونههای آشنایی از فرآیندهای خودبخودی:
- گازی که کل ظرف را در بر میگیرد.
- حبه قندی که در فنجانی از قهوه حل شده و در کل فضای فنجان پخش میشود.
- لیوان نوشیدنی که به زمین برخورده و تکههای شکسته آن در زمین پخش میشود.
- تکه یخی که در کاسهای از آب گرم ذوب میشود.
- توپ پلاستیکی که پس از هر دفعه برخورد با زمین از ارتفاع برگشتش کم میشود.
در هیچ یک از مثالهای واکنش خودبخودی، عکس روند توضیح داده شده در مثالها رخ نمیدهد. یعنی اینکه مولکولهای گاز هیچگاه خودبهخود در فضایی محدود جمع نمیشوند، قندی که در یک فنجان قهوه حل شده هیچگاه ذراتش دوباره خودبه خود فرم حبه را نمیگیرند و غیره. یک جهت واکنش حود به خودی صورت گرفته و عکس آن جهت هیچگاه حودبهخودی انجام نمیپذیرد.
انتروپی و کمیتهای مقداری
برای ایجاد کمیتی ترمودینامیکی که بتواند اطلاعاتی را در مورد خودبهخودی بودن واکنش در اختیار ما بگذارد(که بعدا تحت عنوان انتروپی معرفی میشود)، ابتدا باید احتمال را در نظر بگیریم چون همانطور که در مثال گازهای ایدهآل شرح داده شد، فرآیندهای خودبهخودی همواره میل به ماندن در وضعیتی با احتمال بالا را دارند.
همه توابع انرژی که در ترمودبنامیک وجود دارد، جزو کمیتهای مقداری هستند. این توابع شامل انرژی درونی (U)، آنتالپی (H)، انرژی Helmholtz (A) و انرژی آزاد گیبس (G) میباشد. ازآنجایی که تابعی که از آن برای اندازهگیری مقدار خودبهخودی بودن استفاده میشود، از واحدهای انرژی استفاده نمیکند، رفتار این تابع مشابه توابع انرژی خواهدبود؛ بنابراین، ما به دنبال کمیت مقداری برای اندازهگیری مقدار خودبهخودی بودن هستیم.
اثبات مقداری نبودن احتمال کار سختی نیست. برای مثال، مولکولهای گاز ایدهآل را که در موارد قبل مثال زده بودیم، درنظر بگیرید، با افزایش اندازه سسیتم از N=1 به N=3 مولکول، احتمال یافتهشدن مولکولها در یک طرف ظرف از (۲/۱) به ۳(۲/۱) کاهش پیدا میکند. در حالیکه در یک کیمت مقداری، با افزایش ۳ فاکتوری اندازه یک سیستم، باید متغیر هم به همان طریق افزایش یابد.
با اینکه احتمال خودش یک کمیت مقداری نمیباشد، تابع یک احتمال ممکن است مقداری باشد. بنابراین در ابتدا لگاریتم طبیعی یک احتمال را در نظر میگیریم. درمثال قبلی، با افزایش اندازه یک سیستم از N=1 به N=3 مولکول، لگاریتم طبیعی احتمال یافته شدن مولکولها در یک طرف ظرف از ln(1/2) به ln(1/2)۳ میرسد.با استفاده از خواص لگاریتم، نتیجه N=3 برابر با ۳ln(1/2) خواهدبود، که سه برابر مقدار N=1 میباشد. بنابراین، لگاریتم طبیعی یک احتمال یک متغیر مقداری است چون رابطه خطی با اندازه یک سیستم دارد.
تعریف آماری انتروپی
Ludwig Boltzmann اولین بار مفهوم آماری این متغیر تازه کشفشده دینامیکی را ارائه کرد که انتروپی نامیده شده و با S نشان داده میشد. معادلهای که برای انتروپی ارائه دادهبود، در سنگقبر وی حک شدهاست.

در نوشتار امروزی، تعریف آماری انتروپی S برابر است با:
S=kB ln W
در این معادله، kB ثابت بولتزمن( برابر با ۱.۳۸۱×۱۰–۲۳ J/K) و W احتمال آن را نشان میدهد. واحد kB ، همانند انتروپی J/K میباشد.
به طور دقیقتر، در تعریف بولتزمن از انتروپی، احتمال W با تعداد سطوح انرژی قابل دسترس برای سیستم مرتبط است. بنابراین، ما درمورد یک فرآنید خودبهخودی به عنوان یک جز واحد در یک سیستمی که از وضعیتی با احتمال کم به وضعیتی با احتمال بالا در حال گذر است، صحبت میکنیم. به عبارت دیگر، سیستم از وضعیتی با انرژی قابل دسترس کم به وضعیتی میل میکند که تعداد سطوح انرژی بیشتری در آن قابل دسترس باشد.
نمونهای از محاسبات آماری انتروپی: مثال انبساط گاز ایدهآل
در اولین مثال کاربردی از تعریف اماری انتروپی، انبساط همدمای یک گاز ایدهال از حجم V۱ به حجم V۲ را در نظر بگیرید. ما میخواهیم از تعریف اماری انتروپی استفاده کنیم تا مفدار تغییرات انتروپی را در هنگام انبساط همدمای گاز ایدهآل را حساب کنیم. بنابراین، S۱ برابر خواهد بود با:
S۱=kBlnW۱
مشابه آن S۲ نیز برابر خواهدبود با:
S۲=kBlnW۲
در اینجا، W۱ نشاندهنده احتمال یافتهشدن N ذره در حجم V۱ از کل حجم VT میباشد و W۲ نشاندهنده احتمال یافتهشدن N ذره در حجم V۲ از کل حجم VT میباشد. با توجه به احتمالهایی که در مثالهای قبلی یافتهشد، میتوانیم آنها را به صورت:
W۱=(V۱/VT)N
و
W۲=(V۲/VT)N
بنویسیم. انتروپیهای حالتهای اولیه و نهایی بدین صورت:
S۱=kBln(V۱/VT)N=NkBln(V۱/VT)
و
S۲=kBln(V۲/VT)N=NkBln(V۲/VT)
خواهدبود. با استفاده از این روابط، تغییرات انتروپی ΔS برای انبساط همدمای گاز ایدهآل از حجم V۱ به حجم V۲ برابر است با:
ΔS=S۲-S۱
=(NkBln(V۲/VT) – NkBln(V۱/VT
=[(NkBln[(V۲/VT)/(V۱/VT
(ΔS=NkBln(V۲/V۱
در اخر، ما میتوانیم از رابطه میان ثابت گازی R، عدد آووگادرو NA، و ثابت بولتزمن kB استفاده کنیم،
R=NAkB
بنابراین، فاکتور NkB در معادله تغییرات انتروپی را میتوان به صورت زیر نیز نوشت:
NkB=NR/NA=nR
که n در این معادله تعداد مولها را نشان میدهد. بنابراین، شکل نهایی معادله تغییرات انتروپی برابر خواهدبود با:
(ΔS=nRln(V۲/V۱
برای بدست آوردن این نتایج، علاوه بر استفاده از تعریف اماری انتروپی، از این فرض نیز استفاده شده که تغییرات انتروپی فقط به حالتهای اولیه و نهایی سیستم بستگی دارد.
